Adaptive optics
Introduction
"Adaptive Optics (AO) is a scientific and engineering discipline whereby the performance of an optical signal is improved by using information about the environment in which it passes." [1]
In Astronomical applications the medium is the Earth's turbulent atmosphere, and the optical signal is the light emitted by the star or body of interest. Small temperature fluctuations in the atmosphere create turbulent layers and vary the density of the atmosphere. The effects of this on light that passes through the atmosphere are threefold. Firstly it creates intensity fluctuations (or scintillation) which is observed as the 'twinkling' of the stars. Secondly the position of the star 'wanders' when the varying refractive index of the atmosphere alters the angle of arrival of the starlight. Lastly, there is a spreading effect created by the higher order aberrations which causes stars to appear as small discs of light and not sharply defined point sources [2]. These unwanted aberrations and distortions to the wavefront must be removed, the process of doing this is known as adaptive correction.

Astronomers at the Very Large Telescope (VLT) site in Chile are trying to measure the distortions of Earth's ever changing atmosphere. Constant imaging of high-altitude atoms excited by the laser which appears like an artificial star allow astronomers to instantly measure atmospheric blurring. This information is fed back to a VLT telescope mirror which is then slightly deformed to minimize this blurring. In this case, a VLT was observing our Galaxy's centre, and so Earth's atmospheric blurring in that direction was needed. The beam is almost invisible to the naked eye. The photograph was taken over a period of time thereby making the beam visible.
back to top
AO systems
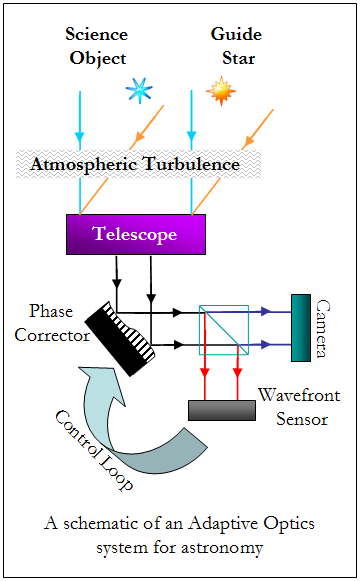
There are two main types of AO system: ones which provide real-time dynamic correction of unwanted optical aberrations, and ones which can manipulate the properties of an optical system to deliver a desired output. The former is used, for example, in applications in astronomy, ophthalmology, military imaging and confocal microscopy. The latter type of AO system can be used, for example, in the measurement and manipulation of laser beams in laser materials processing.
In either case all AO systems comprise 3 main parts; the wavefront sensor, the deformable mirror/corrective element and the feedback loop/actuator control loop. Phase Diversity (PD) wave front sensing refers to the process of retrieving the phase of the distorted wavefront and using that to improve the quality of the image. PD wavefront sensing has formed the basis of several HW WAF research grants.
A schematic of an AO system is shown in figure opposite. In this example, when light enters the system a small amount is taken to the wavefront sensor (via the beam splitter). This is the used to analyse the aberrations on the wavefront. When these have been calculated a corrective signal is sent to the deformable mirror which then changes shape to correct the incoming light. The light used to probe the aberrations comes from the guide star (GS) which can be the observed star, or if it is too dim a bright nearby star or an artificial laser GS is used.
AO systems are already in place, and working to great effect, on some of the present generation of large telescopes. As telescope size increases so too does the challenge faced by AO mainly due to the increased number of modes needed to describe the larger wavefront.
AO is considered a critical development area for the next generation of telescope [3].
back to top
Mathematical description and phase conjugation

Often a key step in performing phase retrieval, or applying phase correction, is to choose a method to express the shape of the wavefront.
The wavefront is a two-dimensional map of the phase of the optical signal and there are two main methods to describe this mathematically; power series (in polar co-ordinates) and Zernike Polynomials. The latter has the advantage of being an orthonormal set over circular apertures. Many of the applications which require adaptive correction use circular apertures, for example telescope and lens systems, making Zernike polynomials a convenient way to express the wavefront. The Zernike series contains a term for each aberration and has the distinct advantage that the rms (root mean square) error can be easily calculated using a geometric sum [1]. This convenient method of expressing an aberrated wavefront can then be used as the input to a corrective element (such as a deformable mirror) that can then apply the opposite distortion thus cancelling out its effect on the wavefront. This process is known as phase conjugation (i.e. multiplying by the complex conjugate of the distortion). The figure above shows an example of a high-order zernike polynomial (Z64).
back to top
References
- Tyson, R.K., Principles of Adaptive Optics. 1st ed. 1991, London: Academic Press Ltd. 260.
- Lukin, V.P., Atmospheric Adaptive Optics. 2nd ed. 1995, Washington: SPIE Optical Engineering Press. 249.
- Gilmozzi, R. and P. Dierickx, OWL Concept study, in ESO Messenger. 2000.
back to top
Resources
In this section you'll find background information for our research interests (past and present) and useful links to other sites.