Phase reconstruction
This is a brief introduction to the topic of phase reconstriction. The interested reader should obtain copies of the papers mentioned to learn more. There are also some documents and presentations that can be downloaded from this page that were created for HW WAF's use but which also provide background information.
Background information:
- When is reconstruction required?
- Reconstruction methods
- Iterative or Analytic?
- Examples of both types
Algorithms that we have used in the past:
For defocus-only based systems:
- Defocus phase diveristy data reduction - introduction
- The Green's function solution
- The Gureyev-Nugent algorithm
The way forward?...
To reconstruct or not to reconstruct?...
For wavefront sensing it can be desirable (although not always necessary) to reconstruct the phase of the wavefront under test. This can involve significant computation time depending on the algorithm that you use. For most Adaptive Optics (AO) applications so long as the signal produces gives sufficient information to drive a corrective element, there is no need to resolve the wavefront phase into all its component modes.
However, there are applications where full reconstruction is useful. In metrology the wavefront shape may be caused by reflection from a surface whose profile is to be measured. The aberrations of optical systems or single components could also be tested by performing a full reconstruction.
The conclusion is that full wavefront reconstruction certainly does have its uses, but if it is not strictly needed then there is no reason to increase the computation time by doing a full reconstruction. It is left to the user to decide what information is needed from the system, whether to calculate the reconstruction throughout or perhaps just as a 'before' and 'after' test to see how well the AO system has performed the compensation.
back to top
Reconstruction methods
There exist a vast number of algorithms for the reconstruction of a wavefront, most commonly using measurements of its local slope or curvature taken using intensity images from the testing system. Retrieval of the phase of an unknown wavefront from intensity images can yield important information about the object which generated the radiation, the quality of the optical system used to form the image and the aberrations the wavefront suffered between emission and detection. Whole books could be written on this topic so it won't be covered in any detail here, instead this page will introduce some basic background about the phase retrieval methods that we have successfully used ourselves.
back to top
Iterative or Analytic?
Phase retrieval algorithms can, for the most part, be divided into 2 sub-categories; iterative and analytic. The relative merits of each type will be briefly reviewed here.
Iterative solutions to the phase problem involve choice of an error metric - a measure of the quality of the computed solution - and will continue to refine the solution until a predetermined minimum in this metric is found. If the solution converges, which is in itself not guaranteed and has to be investigated for each method, there are still many issues to be considered. One such issue is whether the solution found is a global or a local minimum. To ensure it is a global minimum, algorithms of increasing complexity have been produced which, rather than using a simple hill-climbing method, employ a genetic algorithm (GA) approach. In contrast to other numerical techniques which iteratively refine a single solution, genetic algorithms work in parallel testing many possible solutions at once. The advantage of this is that it is far more likely that global minima will be found, the disadvantage is that it often takes a long time to converge and because of the stochastic nature of GA's the global minima found is actually an estimate not an accurate solution. Perhaps the main problem when choosing to use an iterative algorithm is the computational expensiveness of it. The algorithm may converge, and it may be a guaranteed global minimum, but if this requires excessive amounts of computer equipment or if it takes an unreasonable length of time to provide the solution then it will not be suitable.
Analytical solutions can be faster to compute and usually don't require complicated minima search techniques as they essentially go straight to the final answer. The question then becomes whether this is the right answer or not, assumptions may have been made when deriving the analytic solution which then limit its accuracy. Computational expensiveness can also be traded for mathematical complexity in the process of designing the algorithm. The user must consider whether the extra time taken to develop an analytical algorithm is appropriate for their application, or if a well known iterative solution will be good enough.
back to top
Examples of both types...
The most widely used iterative algorithms for phase retrieval are compared and reviewed by Fienup [1] , these are the error-reduction algorithm, the Gerchberg-Saxton algorithm, the method of steepest descent, conjugate gradient methods and the input-output algorithm. In this paper he concluded that the error reduction algorithm (for single intensity images) and the Gerchberg-Saxton algorithm (for two intensity measurements) will converge, but often at a much slower rate than conjugate gradient or input-output algorithms. There exist a great many algorithms that are variations of these basic iterative structures [2-5] which can prove very effective although in some cases computationally expensive.
Analytical solutions of the Intensity Transport Equation (ITE) [6-8] have been proven to be fast, accurate reconstruction methods for defocus based phase diversity wavefront sensing. A couple of these are covered in more detail below. We are currently working towards the creation of a new analytic solution for Generalised Phase Diversity (GPD), which is also covered below.
back to top
Algorithms that we have used:
Error Reduction algorithm
The Error Reduction algorithm is particularly useful when looking for some quick preliminary results. As mentioned before though, it is not guaranteed that this algorithm will converge. For the applications we have applied it to we found it to work well, and converge in a reasonable length of time (of course this also depends on the computer it's run on!). It works simply by generating a random input wavefront, applying the chosen diversity to it, and calculating the intensity images that would be created by this wavefront in the real optical system. These calculated images can then be compared to either experimentally measured images, or ones created by a simulated wavefront. The algorithm seeks to reduce the error between the calculated and 'real' intensity images, by modifying the input wavefront it creates, until a close match is obtained. In the case of an experimental setup when the match is obtained the final computed wavefront should be the actual wavefront you wished to measure. In the simulated case the user can compare the final computed wavefront with the known simulated wavefront to see how close the fit actually is. This method can be applied to any pair of intensity images, regardless of the diversity condition under which they were recorded. This makes it useful for getting some initial results from simulated GPD data.
HW WAF alumnus Dr Sijiong Zhang prepared a presentation, for our weekly group meeting, about simulations he conducted using the Error Reduction Algorithm and Fractional Fourier Transforms. If you are interested you can download this presentation using the link below:
Error Reduction Algorithm Applied in the Fractional Fourier Domain, by S. Zhang, PDF
back to top
Reconstruction methods for defocus based phase diversity systems
Phase diversity wavefront sensors traditionally use defocus as the diversity phase that is applied to the input wavefront. This can be easily achieved by a variety of methods including; translation of the camera, a vibrating mirror to alter the path length, a beam-splitter dividing the beam into two arms with separate cameras....and so on. One possible setup is shown in the diagram below:
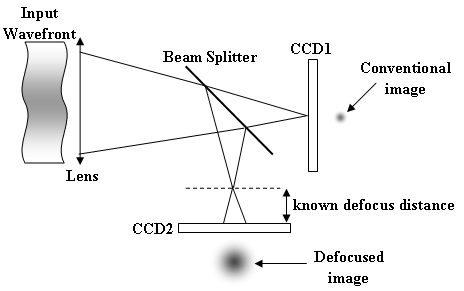
A simple arrangement to record defocus phase diversity sensing data. There are many possible solutions to gather the required data, with factors such as cost, complexity, and ease of use helping the user to choose the best system for their application.
It has also been shown that defocused images can be created and imaged onto a single image plane by use of a diffraction grating [14]. More can be read about this method in the wavefront sensing resources page. Using a diffraction grating has the advantage of being robust, cost-effective, requires only a single camera, and is simple to align.
The Intensity Transport Equation (ITE) may then be solved by taking the difference of a pair of defocused intensity images to give a solution for the phase. More information on this may be found in the wavefront sensing resources page under the heading 'Obtaining the wavefront'.
There are several algorithms that may be used to reconstruct the wavefront phase by solution of the ITE. Two of the algorithms that we have used detailed below...
back to top
Green's Function Solution
The Green's Function Solution to the ITE is an analytic method which used the difference of two intensity images (with equal amounts of diversity but one with +ve defocus, and one with -ve defocus) and a pre-computed Green's function matrix multiplier to reconstruct the phase. A great deal of effort went into the calculation of the Green's matrix, but the advantage is that this same matrix may be used for all experiments. The algorithm then only has to perform a matrix multiply, which multiplies each matrix element of the Green's function with a pixel in the difference image. This makes it an extremely fast method of phase retrieval, and it has been shown to be capable of measuring the curvature of a test wavefront to sub-nanometre precision [9].
Drawbacks
However, there are drawbacks to using this method. Assumptions made about the nature of the wavefront under reconstruction are:
- The wavefront and its first derivative (the slope) must be everywhere continuous within the pupil.
- The illumination must be uniform.
The first assumption means that the performance of the algorithm will be poor if the input wavefront is discontinuous. The second assumption shows that this method is not suitable for scintillated wavefronts.
Motivation for finding a new solution...
Applications like imaging and phasing of segmented telescope mirrors or metrology of integrated circuits would not be possible using this method, due to the first assumption. This assumption also potentially precludes the use of pixellated corrective elements (like liquid crystals) in AO systems, which offer light-weight, robust and cost effective operation. The second assumption renders this method unsuitable for atmospheric measurements with scintillation (in military applications for example), and in polishing applications where a laser is used to illuminate a roughened surface (thus creating speckle).
It is to avoid these assumptions that we started researching alternatives to defocus only phase diversity, and new ways of dealing with the data generated. This new solution - named the 'Small Angle Expansion' (SAE) - is covered below, and offers an alternative to reconstructing defocus-only data as well as GPD data (since GPD can include, but is not limited to, the use of defocus as the diversity function).
back to top
Gureyev-Nugent Algorithm
Another ITE based solution to defocus-only phase diversity systems is offered by the Gureyev-Nugent (GN) algorithm [7,8]. This method uses a modal decomposition of the wavefront to reconstruct the unknown phase. The GN algorithm does this by using matrices, and projecting Zernike modes onto the difference image (formed by a pair of intensity images with equal and opposite amounts of defocus applied). A significant advantage of this algorithm over the Green's function solution is that does not require uniform illumination and so may be used with modestly scintillated wavefronts.
Using the GN algorithm we have reported accuracies in the measurement of a curved wavefront of approx. λ/200 [10]. Similar accuracies have been reported by our collaborators [11] who are using the algorithm to analyze particle tracking data that they have collected using the GPD wavefront sensor.
Disadvantages
The accuracy of this method is highly dependent on the accurate placing of the unit disc onto the difference image. The unit disc is the area over which the algorithm attempts to fit the Zernike modes. If it is not defined to be within a couple of pixels of the boundary of the signal then the computed Zernike coefficients will not be very accurate. This means that for correct application of this algorithm we require either a well trained user to define the boundary (and be consistent over ranges of datasets), or a more sophisticated piece of code to accurately locate the boundaries of the signal. It should be noted that this problem is inherent in any situation where a phase profile is decomposed into a set of modes, and is not unique to the GN algorithm.
More information
HW WAF alumnus Dr Sijiong Zhang prepared a presentation, which he gave at one of our weekly group meetings, about this algorithm. If you are interested you can download this presentation using the link below:
Wavefront reconstruction using the Nugent Algorithm, by S. Zhang, PDF
For a quick summary of how the algorithm works I have created a flow chart showing how the data is generated and which equations are used to solve for the phase. The algorithm was based on the one presented in [7,8]:
Gureyev-Nugent phase reconstruction algorithm: flowchart, by H.I.Campbell PDF
back to top
The way forward?...
SAE ~ An Analytic Solution for GPD
Generalised Phase Diversity (GPD) is so named because it works by applying aberration functions other than just defocus to create phase diverse data. The functions which may be used are limited only by certain symmetry conditions which we have outlined in detail in our Optics Letters paper (a PDF of this can be downloaded below...).
Importantly this means that for non-defocus based GPD, solution of the wavefront phase will no longer be a case of solving the ITE. Our aim was to produce is an analytic solution (and software) to retrieve the unknown phase. This solution, known as the Small Angle Expansion (SAE) is the result of linearising the error signal expression given in the Optics Letters paper, given a wavefront with weak phase (i.e. small phase angle).
By breaking away from the ITE, and avoiding making similar assumptions, the SAE can in principle deal with discontinuous and scintillated wavefronts. It should be pointed out though, that if the user wishes to decompose the wavefront into Zernike coefficients then this algorithm will face the same issues that the GN algorithm did, namely the correct definition of the unit disc (the area over which you fit the solution). This will be a limiting factor in the accuracy of the algorithm.
We have already published results [12,13] that show the SAE working in simulation and with some preliminary experimental results from our diffraction grating based wavefront sensor. For an in-depth description of the SAE and it's usage you can download the PhD thesis of HW WAF alumnus Dr Heather Dalgarno (nee Campbell) using the link below.
GPD Paper:
Campbell, H. I., S. Zhang, et al., Generalised Phase Diversity, Optics Letters 29(23): 2707-2709. (2004) PDF**
**This paper was published in Optics Letters and is made available as an electronic reprint with the permission of OSA. The paper can be found at the following URL on the OSA website: http://www.opticsinfobase.org/ol/abstract.cfm?uri=ol-29-23-2707. Systematic or multiple reproduction or distribution to multiple locations via electronic or other means is prohibited and is subject to penalties under law.
For more information...
On GPD and the SAE, see:
Generalised Phase Diversity Wavefront Sensing, PhD Thesis, H.I.Campbell, Heriot-Watt University, School of Engineering and Physical Sciences, 2006, PDF
back to top
References
- J.R. Fienup, Phase Retrieval Algorithms: a comparison, Appl. Opt., 21(15), p.2758-2769, 1982.
- N. Baba, H. Tomita, and M. Noriaki, Iterative reconstruction method in phase diversity imaging, Applied Optics, 1994. 33(20), p.4428-4433.
- N.Baba and K. Mutoh, Measurement of telescope aberrations through atmospheric turbulence by use of phase diversity, Appl. Opt., 40(4), p.544-552, 2001.
- J.R. Fienup and A.M. Kowalczyk, Phase Retrieval for a Complex-Valued Object by Using a Low- Resolution Image, JOSA A, 7(3), p.450-458, 1990.
- V.Y. Ivanov, V.P. Sivokon, and M.A. Vorontsov, Phase retrieval from a set of intensity measurements:theory and experiments, JOSA A, 9(9), p.1515-1524, 1992.
- S.C. Woods and A.H. Greenaway, Wave-front sensing by use of a Green's function solution to the intensity transport equation, JOSA A, 20(3), p.508-12, 2003.
- T.E. Gureyev, A. Roberts, and K.A. Nugent, Phase retrieval with the transport-of-intensity equation: matrix solution with use of Zernike polynomials, JOSA A, 12(9), p.1932, 1995.
- T.E. Gureyev and K.A. Nugent, Phase retrieval with the transport-of-intensity equation. II. Orthogonal series solution for nonuniform illumination, JOSA A, 13(8), p.1670, 1996.
- S. Djidel and A.H. Greenaway. Nanometric wavefront sensing, in 3rd International Workshop on Adaptive Optics in Industry and Medicine, Starline Printing Inc., 2002
- H. I. Campbell, S. Zhang, et al., Generalised Phase Diversity Wavefront Sensing, AMOS Technical Conference, Wailea, Maui, USA 13-17th September 2004. PDF
- Towers C.E, Campbell H.I, Zhang S., Greenaway A.H., Towers D.P. Wavefront Sensing for Single View 3-Component 3-Dimensional Particle Imaging, 6th International Symposium on Particle Image Velocimetry in Pasadena, California (21/09/05-23/09/05)
- H.I. Campbell , S.Zhang , Greenaway A.H, Extending Wavefront Sensing with Novel Diversity Functions, Proc. SPIE Vol. 6018, p.201-209
- S. Zhang, H.I Campbell, Greenaway A.H, Small Angle Expansion, A Solution to the Phase-Retrieval Problem Using Generalised Phase Diversity in Pupil Space, Proc. SPIE Vol. 6018, p.390-398
- Blanchard, P.M. and A.H. Greenaway, Simultaneous multiplane imaging with a distorted diffraction grating, Applied Optics, 1999. 38(32): p. 6692-6699.
back to top
Resources
In this section you'll find background information for our research interests (past and present) and useful links to other sites.