Optical aperture synthesis
Introduction
Optical Aperture Synthesis (OAS) offers the possibility to achieve surveillance images with more than 100x the information content or 10x the range of current equipment. Our research in this area included an initial study of the risks associated with implementation of OAS in military applications and examined both passive and active synthesis imaging methods.
On this page you will find a brief mathematical description behind the principle of optical aperture synthesis and suggestions for further reading.
back to top
The complex visibility
The complex visibility of an interference pattern produced by a pair of apertures (i.e. one particular baseline vector) is one particular Fourier component of the source brightness distribution (from the Van Cittert Zernike theorem). You can use a range of baselines i.e. aperture separations to obtain a range of spatial frequencies. The measured complex visibility is otherwise known as the mutual coherence function, which is given by:
when 
becomes 0 we have the mutual intensity or complex visibility:
equation 1
Where:
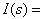intensity in the direction 
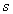where 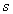is a unit vector.
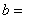the vector separation (baseline vector).
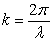is the component of the wave vector in direction
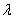is the central wavelength.
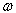is the solid angle.
In aperture synthesis we measure 
at different values of aperture separation 
and we get 
by inversion of equation 1 above.
back to top
The 2-D case
The following is known as the fundamental equation for aperture synthesis:
then given a number of measurements of 
at different points in the UV plane i.e. for different point apertures we need to invert the equation to get 
. Using the inverse FT:
I = 
When only measured at a limited number of points in the UV plane we need to replace the integral by the summation:
W is a weight factor associated with the jth point. Then 
is the “dirty map” it is the convolution of the true I with a point spread function. So:
In practice the complex visibility includes instrumental and environmental perturbation effects which produce phase errors. Individual aperture phase errors may be eliminated by summing the phases round a closed loop of baselines i.e. phase closure. However phase closure should really only be applied to situations where signal to noise ratio is poor, otherwise it is rather an inefficient method of aperture synthesis. We are demonstrating the use of Redundant Spacings Calibration instead. This method is based on the principle that when the target is a large distance away the information collected by identical aperture pairs or baselines should be the same. Any difference arising must therefore be due to localised phase errors such as in atmospheric turbulence or in system calibration and a single aperture involved in a redundant baseline can be "driven" so as to match the phase of the resulting interference fringes. This self-calibration of the system can be done in a very small time scale without the need for "off-line" computations, again making it ideal for use in mobile imaging systems.
The phase relations can be regarded as a set of matrix equations to which there are more unknowns than knowns. Introducing redundant conditions makes the matrix full rank and a unique solution can be achieved.
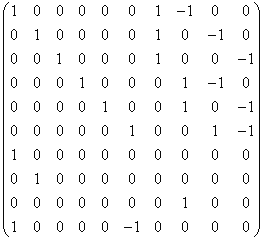
This method does not give absolute object phase information. A relative phase plane is defined by three apertures and the rest are driven to match. However absolute phase information is not essential to reconstruct the image.
The principle of using multiple collecting apertures to sample an object can be used in reverse in a technique called Fourier telescopy. Whereby an array of apertures are used to project interference fringes of varying spatial frequency onto the target and by applying a phase shift to displace the interference pattern by π radians, a camera can integrate up the reflected light and the data collected is then exactly the form of the object's Fourier transform. This technique allows high resolution images to be taken from low resolution quality optics even with a wide field of view, gives high signal to noise ratio independent of resolution and can be used with RSC. This is useful in many aspects of metrology.
Because source coherence is required to produce a spatially coherent interference pattern on the target, laser speckle becomes an issue.
back to top
Further Reading
- A.H. Greenaway, Optical Aperture Synthesis, Meas. Sci. Technol. 2, 1991.
- A.H. Greenaway, Terrestrial optical aperture synthesis technique (TOAST), Opt. Comm., 58(3), p.149-154, 1986.
- A.H. Greenaway, A.M. Johnson, A. Harvey, et al., Optical Aperture Synthesis, 1st Annual EMRS DTC Conference, Edinburgh, May 2004.
- P.W. Gorham, Designing Optimal Bandwidth Synthesis Arrays for VLBI, TIMO progress report 42-133, May 1998.
- T.J. Pearson and A.C.S. Readhead, Image formation by self-calibration in radio astronomy, Ann. Rev. Astron. & Astrophys., 22, p.97-130, 1984.
- R.C. Jennison, A phase sensitive interferometer technique for the measurement of the Fourier transforms of spatial brightness distributions of small angular extent, 1958
- M. Ryle and A. Hewish, The synthesis of large radio telescopes, August 24 1959
- S.K. Saha, Emerging trends of optical interferometry in astronomy, Bull. Astron. Soc. India 27, p.441-546, 1999.
- V.I. Mandrosov, Fourier telescopy imaging through strongly inhomogeneous atmosphere at high level of additive noises, Proc. SPIE Vol. 4538, p128-134
- Born & Wolf, Principles of Optics, 7th expanded edition, Cambridge Press, 1999.
- J.W. Goodman, Introduction to Fourier Optics, 2nd Edition, McGraw-Hill, 1996.
back to top
Resources
In this section you'll find background information for our research interests (past and present) and useful links to other sites.